A function can solve a task by calling other functions or itself. It is a chalk of tasks that is split into smaller or several tasks of the same kind.
Every function solves a task.
See the example below:
const pow = (x, y) => {
if (y === 1) {
return x;
}
return pow(x, y - 1) * x;
};
console.log( pow(2, 4) ); // 16
Iterative thinking
const pow = (x, y) => {
let result = 1; // y = 0 => x⁰ = 1
for (let i = 0; i < y; i++) {
result *= x; // result = result * x; from Y = (i0 < y) to Y = y-1
// at constant x of 2
// result(i0) = result * 2 = 2; for Y = y - 4 (y=4, Y=0)
// result(i1) = result * 2; => result(i0) * 2 = 4; for Y = y - 3 (y=4, Y=1)
// result(i2) = result * 2; => result(i1) * 2 = 8; for Y = y - 2 (y=4, Y=2)
// result(i3) = result * 2; => result(i2) * 2 = 16; for Y = y - 1 (y=4, Y=3)
}
return result;
// result(y) = result * 2; => 16
// (2⁴ = 2 * 2 * 2 * 2 = (2 * 2 * 2) * 2 = 2³ * 2 )
// where y = 4; y - 1 = 3
};
console.log( pow(2, 4) ); // 16
Recursive thinking
In the example above, what if the result from i0 to i2 is the repeated calling function.
It is obvious also that x¹ is x. This means at let result = 1, we can make let y = 1 has the base recursion.
See the example below:
const pow = (x, y) => {
if (y === 1) {
return x; // base => x¹ = x
}
// Alternatively
/*
if (y === 0) {
return 1; // base => x⁰ = 1
}
*/
else {
return pow( x, (y-1) ) * x; // x(y) = x(y-1) * x
}
};
console.log( pow(2, 4) ); // 16
The proof above is xy = x or xy = xy-1 * x
The above example can be re-written as shown below:
const pow = (x, y) => {
return (y === 1) ? x : ( pow(x, y - 1) * x );
};
console.log( pow(2, 4) ); // 16
In the example above pow(x, y) === pow( x, (y-1) ) * x i.e. x<sup>y</sup> === x<sup>y - 1</sup> * x. In math it is called recursive step. The step continues still y = 1. That is still pow(x, y) === pow( x, (1 - 1) ) * x
The expression pow(x, y) === pow( x, (0) ) * x is the same as x0 * x which is x. In math x0 = 1.
Every recursive function must have a base.
In each step of the recursive function, we have the following calls
pow(2, 4) = pow(2, 3) * 2 // first step
pow(2, 3) = pow(2, 2) * 2 // second step
pow(2, 2) = pow(2, 1) * 2 // third step
pow(2, 1) = pow(2, 0) * 2 = 2 // forth step
For iterative thinking, the steps are in reverse.
pow(2, 1) = pow(2, 0) * 2 = 2 // first step
pow(2, 2) = pow(2, 1) * 2 // second step
pow(2, 3) = pow(2, 2) * 2 // third step
pow(2, 4) = pow(2, 3) * 2 // forth step
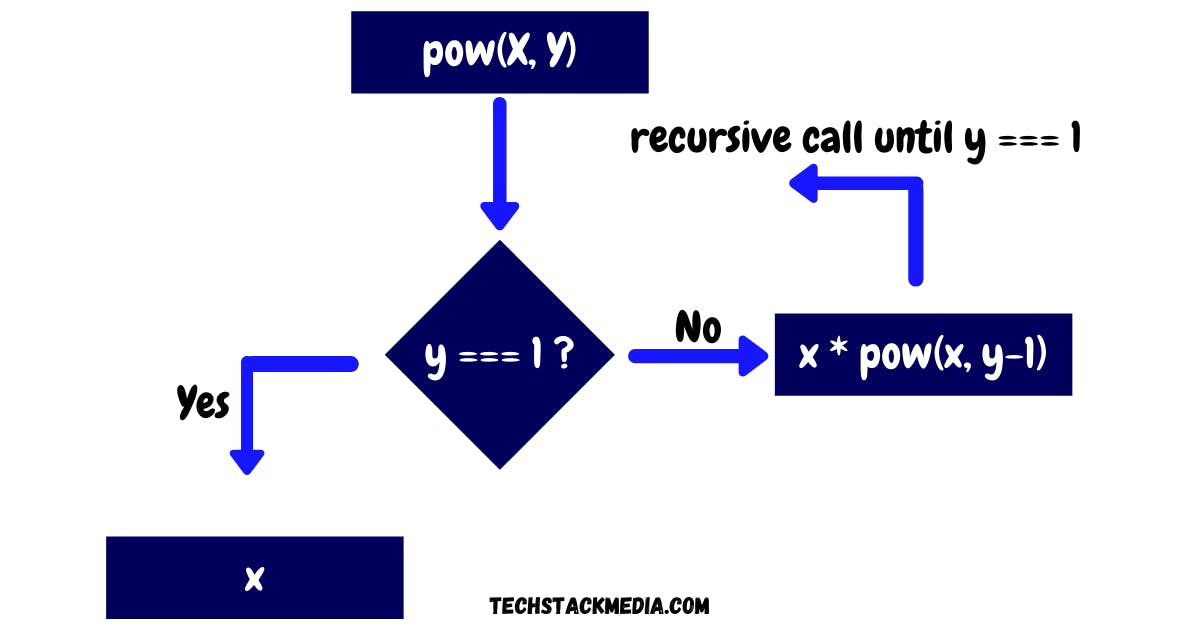
The total number of nesting calls above is y = 4. The total recursive nesting calls is termed recursion depth.
The recursion function has its limitation:
The recursion depth is a factor to consider in the recursive function because the maximum should be less than 100000 in the JavaScript engine. It is recommended to target a max of 1000 though for better optimization.
There are tail calls optimizations that improve the limitation but not yet supported everywhere and work only in simple cases.
It is recommended to use recursive thinking than iterative thinking often for easier and maintainable code
See another example below:
const factorial = num => {
if (num === 0) {
return 1; // base => 0! = 1
} else if (num > 0) {
// 4! = 4 * (3 * 2 * 1) === 4 * 3! === num * (num - 1)!
return ( num * factorial(num - 1) )
} else {
return -1;
}
};
console.log( factorial(4) ); // 24
In the example above, factorial(num) === num * factorial(num - 1)
Since 0! = 1 or 1! = 0, the base can be as shown below:
... ... ...
if (num === 0 || num === 1) {
return 1; // base => 0! = 1
}
... ... ...
... ... ...
... ... ...
Conclusion
With recursion, all you need is to pull out a constant and iterate till the count i = y or i === num


